Ladingontwikkeling – Deel 2

 

In die soeke na ʼn alternatiewe jaglading vir my .308 het ek onlangs ʼn plaaslike koeëlvervaardiger se produk op die proef gestel. Ek gebruik graag S335 kruit van Sonchem en die koeëlgewig was 165gr. Indien hierdie die eerste keer was wat ek 165gr koeëls in my geweer getoets het, sou ek op die naaste koeëlgewigaanbeveling van die kruitvervaardiger (168gr) begin het by 37.4gr en opgewerk het in 0.3gr inkremente tot 41.5gr. Dit het egter oor tyd vir my duidelik geword dat die beste lading op my geweer tussen 40gr en 41.6gr is vir 165gr koeëls. Ek het dit goedgedink om hierdie spesifieke voorbeeld te verduidelik aangesien minder skote gevuur is, maar meer as een potensiële sweet spot visueel ontstaan het. Dit bly onder normale omstandighede uiters belangrik om by die minimum lading te begin skiet en stelselmatig op te werk tot by die maksimum lading. Let ook op vir enige tekens van druk en moet eerder nie ʼn hoër lading afvuur indien tekens van druk ervaar word nie.

 

Die ladder is geskiet op 200m en daar is met elke skoot aangelê op die oranje kol. Vanuit die vertikale verspreiding in Figuur 1 word dit duidelik dat skote 1, 2 en 3 ʼn bondel vorm, dan weer potensieel skote 4 en 5, waarna die groter bondel skoot 6, 7, 8 en 9 is.



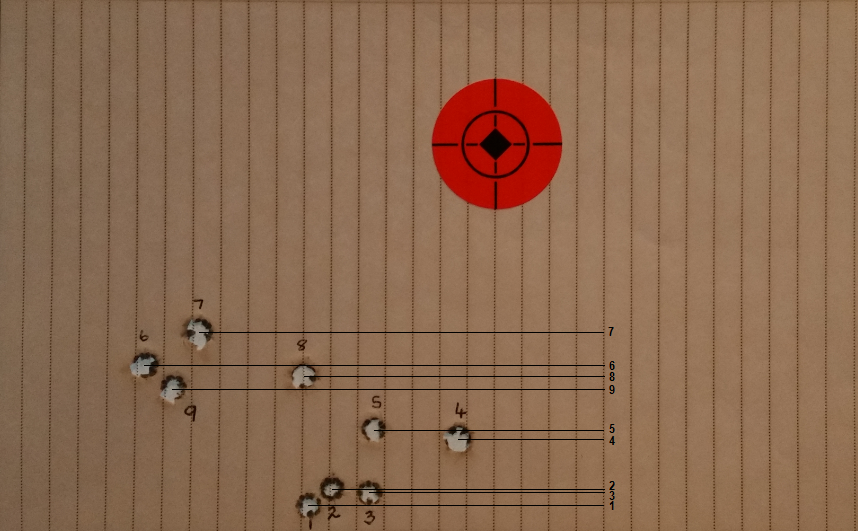
Let asseblief op dat dit nie noodwendig so sal uitwerk dat die skote in numeriese volgorde sal bondel nie en dat skote van verskillende ladings wel oor en weer kan bondel. Dit is egter so dat indien skote van ladings wat op mekaar volg deel vorm van ʼn bondel, dit meer sinvol sal wees om groeperingsladings uit hierdie skote te kies aangesien dit daarop dui dat die opeenvolgende ladings stabiel is en reeds saam bondel. Die oorspronklike teorie sê egter dat mens dan die middelste skoot in die bondel kies en rondom hierdie lading laai om groeperings mee te skiet. 

 

Die keuse van hierdie groeperingtoetslading(s) wat deel vorm van die bondel is gewoonlik nie so maklik nie en verg heelwat ervaring en interpretasie. Dit het my egter genoop om ʼn identifikasie proses vir hierdie groeperingstoetslading saam te stel. My aanvanklike gedagte was dat indien skote bondel, daar een of ander konstante of minimum variasie in die spoed van elk van hierdie skote moes wees. Gelukkig skiet ek meestal oor ʼn chronograaf en kon begin om die spoed van die verskillende ladings te vergelyk met die doel om een of ander tendens te identifiseer. Na ʼn hele paar berekeninge getoets is, het ʼn spesifieke tendens na vore gekom wat gestrook het met vorige ladder resultate. In kort kan die berekening vereenselwig word met die konsep van Absolute Minima en Maksima in Calculus wiskunde. Die toepassing hiervan is egter heel eenvoudig in die geval van ladings ontwikkeling en kan as volg verduidelik word na aanleiding van die bostaande ladder toets.

 

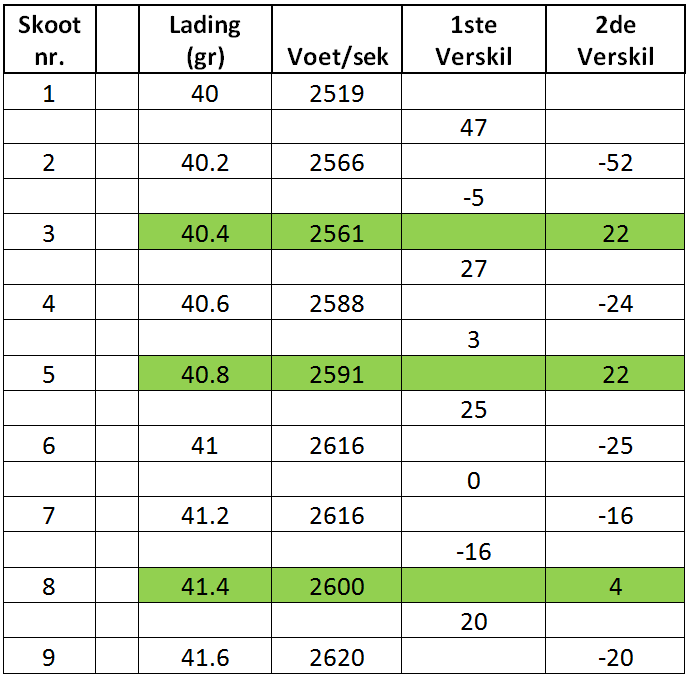
Die eerste stap in hierdie berekening is natuurlik om die lading en elke lading se spoed (gewoonlik in voet per sekonde) van die minimum tot maksimum lading in te vul op die spreivel. Daarna word die verskil in spoed tussen die verskillende ladings bereken in die 1ste Verskil-kolom. Die waarde 47 is slegs (2566 – 2519) en -5 is (2561 – 2566). Die res van die waardes in die 1ste Verskil-kolom word op dieselfde manier bereken. In die 2de Verskil-kolom word die proses herhaal en die verskil van die verskil in spoed word bepaal. Die waarde -52 is slegs  ((-5) – ABS(47)). Die ABS voor die waarde wat afgetrek word is ʼn funksie in Excel en beteken slegs dat die absolute waarde of getal self afgetrek word en dat die teken voor die getal nie in ag geneem moet word nie. Op dieselfde manier is die waarde 22 dan (27 – ABS(-5)). Die res van die waardes in kolom twee word dan dienooreenkomstig bereken.

 

Na afloop van hierdie berekening ontstaan daar dan gewoonlik in die 2de Verskil-kolom ʼn tendens waar die waardes van bo na onder negatief-positief-negatief word. In hierdie spesifieke voorbeeld is daar drie sulke gevalle. Die positiewe waarde of absolute minima van die tendens kan weer teruggetrek word na ʼn spesifieke skootnommer of lading soos aangedui deur die lyne wat in groen ingekleur is. Die eerste geval is (-52 / 22 / -24) met die positiewe waarde 22 wat ooreenstem met skoot 3 of 40.4gr. Die tweede geval is (-24 / 22 / -25) met die positiewe waarde 22 wat ooreenstem met skoot 5 of 40.8gr. Die derde geval is (-16 / 4 / -20) met die positiewe waarde 4 wat ooreenstem met skoot 8 of 41.4gr. Interessant genoeg kan elk van ladings wat geïdentifiseer is met die Absolute Minima metode ook gekoppel word aan ʼn skoot in die visuele ladder bondels soos weerspieël in Figuur 1. 

 

Vanuit hierdie bevestiging het ek dus besluit om skote 3, 5 en 8 as groeperingstoetse te laai. Vier rondtes van skoot 3 (40.4gr), skoot 5 (40.8gr) en skoot 8 (41.4gr) is dienooreenkomstig gelaai en weer op 200m geskiet. Die resultaat van hierdie groeperingstoetse word onderskeidelik in die volgedne figure vervat: 

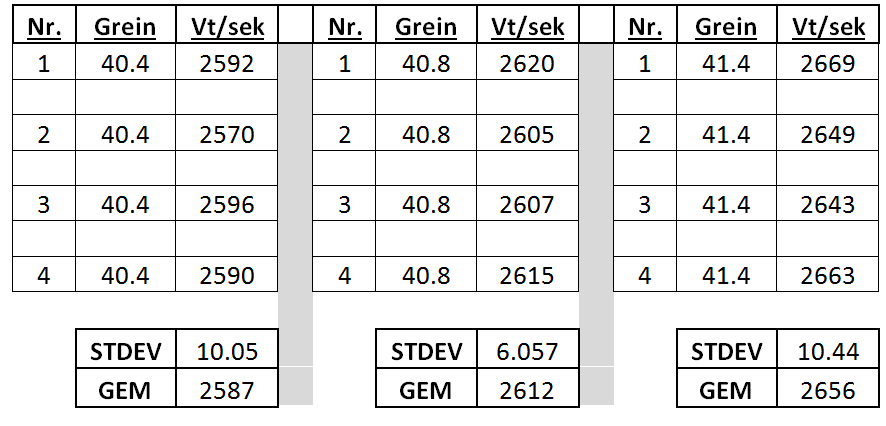
Die spoedresultate van die skote word in Tabel 2 hieronder gelys. Op die ou end het ek besluit op  ʼn lading van 40.8gr aangesien die horisontale en vertikale verspreiding tussen die skote heelwat kleiner was as die ander twee en omdat die standaard afwyking (Stdev) van die spoed tussen die rondtes van dieselfde lading die kleinste was. Ter bevestiging het ek later weer 40.7gr, 40.8gr en 40.9gr groepe gaan toets net om te bevestig dat 40.8gr wel die beter lading vir hierdie kombinasie in my geweer is. 

 

Die belangrikste beginsel kan maklik in die woorde “doen die een en moet die ander nie nalaat nie” saamgevat word. Dit is uiters belangrik dat ʼn skut tydens ladingsontwikkeling oor ʼn chronograaf skiet om die visuele ladder en Absolute Minima berekening apart en gesamentlik te interpreteer. Die node of stabiele punt wat bepaal word deur die Absolute Minima metode dui op  ʼn lading waar die variasie in spoed van die betrokke lading na alle waarskynlikheid stabiel sal wees of geminimaliseer  sal word. Die beste resultate word gewoonlik verkry wanneer die visuele ladder ʼn bondel vorm en die Absolute Minima metode ʼn lading identifiseer wat deel vorm van die bondel. Indien daar meer as een ooreenstemmende lading geïdentifiseer word sal dit raadsaam wees om beide te toets om die beter lading te identifiseer, waarna die ladings 0.1gr weerskante van die mees stabiele lading ook getoets kan word. 

 

Onthou altyd dat veilige en verantwoordelike herlaaipraktyke voorrang moet geniet. Wees dus bedag op tekens van druk en stop onmiddellik as enige tekens van druk ervaar word. Kies altyd akkuraatheid bo spoed tydens ladingsontwikkeling. Maak seker van jou skiettegniek en veral dat die geweerrus stabiel is sodat die wapen elke keer in dieselfde posisie geplaas word voordat ʼn skoot afgevuur word. Elke geweer het sy eie resep en dit is belangrik dat jy deur middel van ʼn gestruktureerde proses by  ʼn optimale lading vir jou geweer uitkom. Afgesien van al die moontlike “kortpaaie” wat kan help om met minder skote by  ʼn akkurate lading uit te kom, bly dit onvermydelik vir ʼn herlaaier om gereeld op die baan uit te kom. Op die ou end raak dit soms moeilik om te onderskei of ʼn herlaaier beter groepe skiet omdat die lading vir sy geweer optimaal  is en of dit is omdat hy meer tyd op die baan spandeer om die kuns van akkuraat skiet te verfyn. Ek hoop van harte dat die metodes soos verduidelik vir jou as mede-herlaaier sinvol sal wees as hulpmiddel om jou geweer se akkuraatheidspotensiaal te verwesenlik.